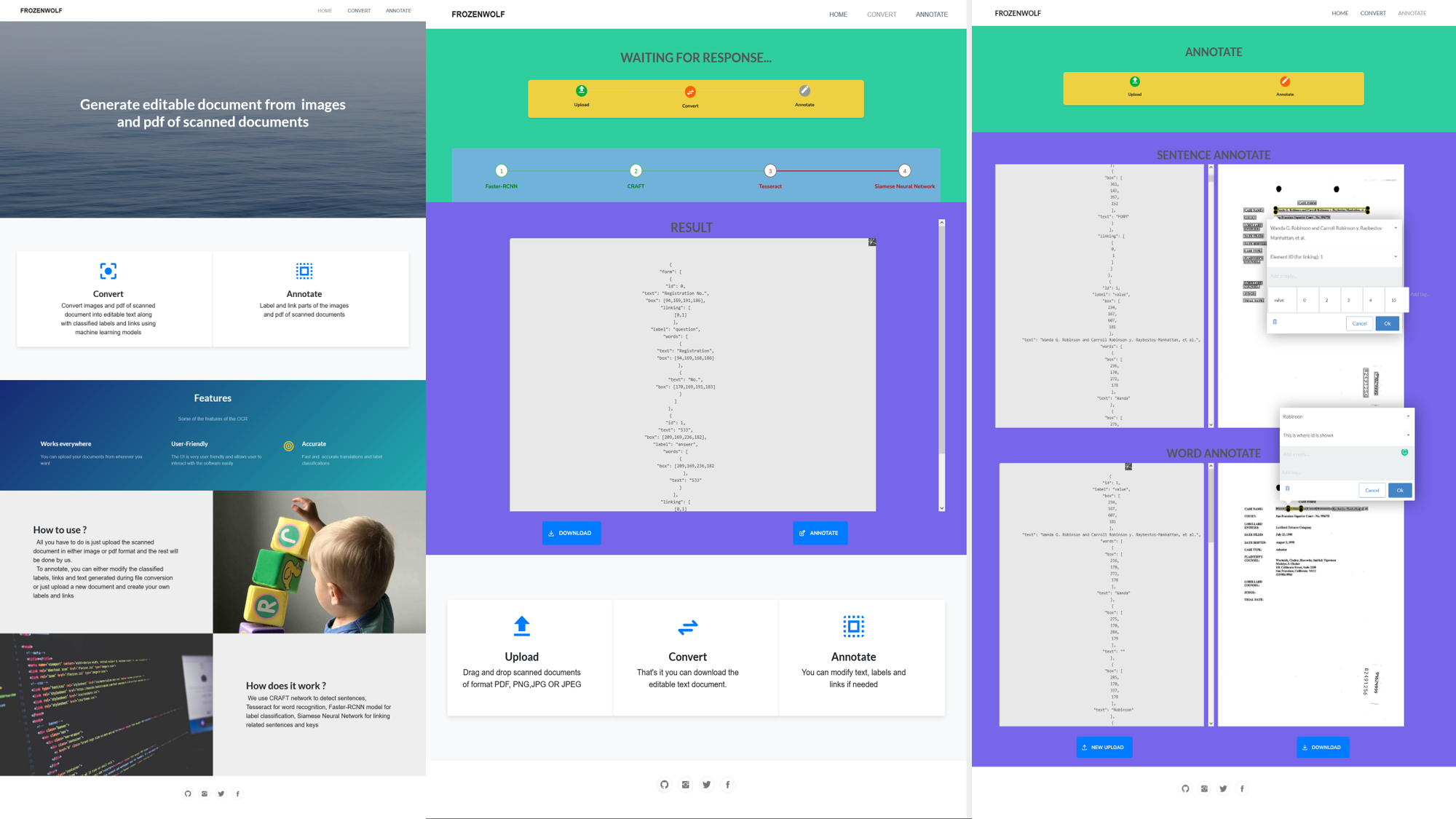
Observations
CTC Benchmarking
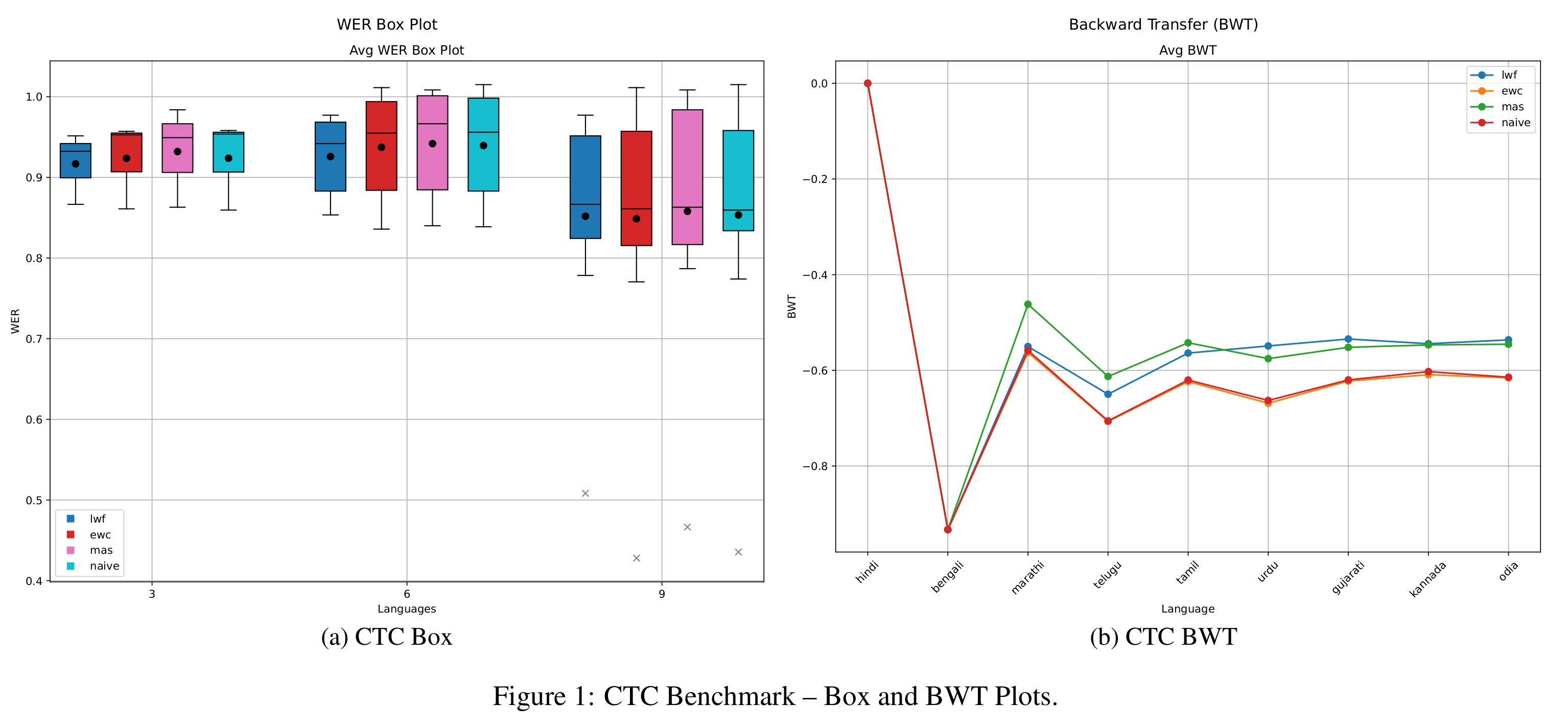
As shown in Figure 1, the average WER across tasks reveals a clear ranking among methods. LwF achieves the best overall performance, followed by EWC, then MAS, with naive fine-tuning performing the worst. This ranking is particularly evident in short and medium task horizons. For longer sequences, however, the performance gap between methods narrows considerably. Naive fine-tuning, in particular, produces the highest WER maxima across tasks. When analyzing backward transfer (BWT), MAS performs best in short sequences, while LwF excels in medium-length tasks. For longer sequences, both MAS and LwF converge to similar average BWT values, whereas EWC and naive fine-tuning fall behind.
RNN-T Benchmarking
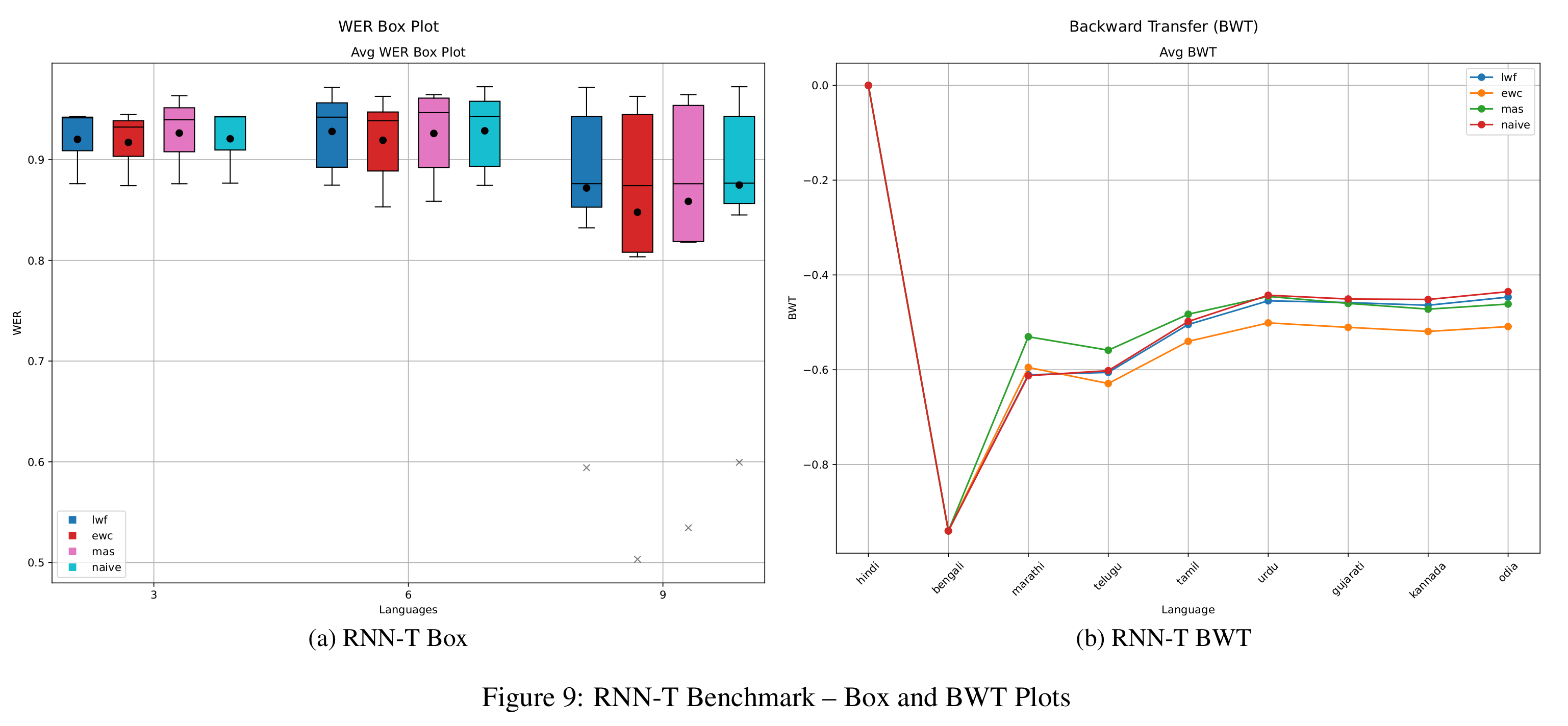
Figure 9 shows that RNN-T consistently outperforms CTC in WER across all continual learning strategies. Among these, EWC achieves the lowest WER across task lengths, demonstrating strong performance retention on the current task. However, this benefit comes at a cost: EWC exhibits the worst BWT of all methods, even lower than that of naive fine-tuning, indicating substantial forgetting. MAS shows some improvement in BWT for medium-length sequences, but for longer horizons, BWT scores deteriorate across all methods except EWC, eventually becoming nearly indistinguishable.
General Comparison of CL Methods under Noisy Settings
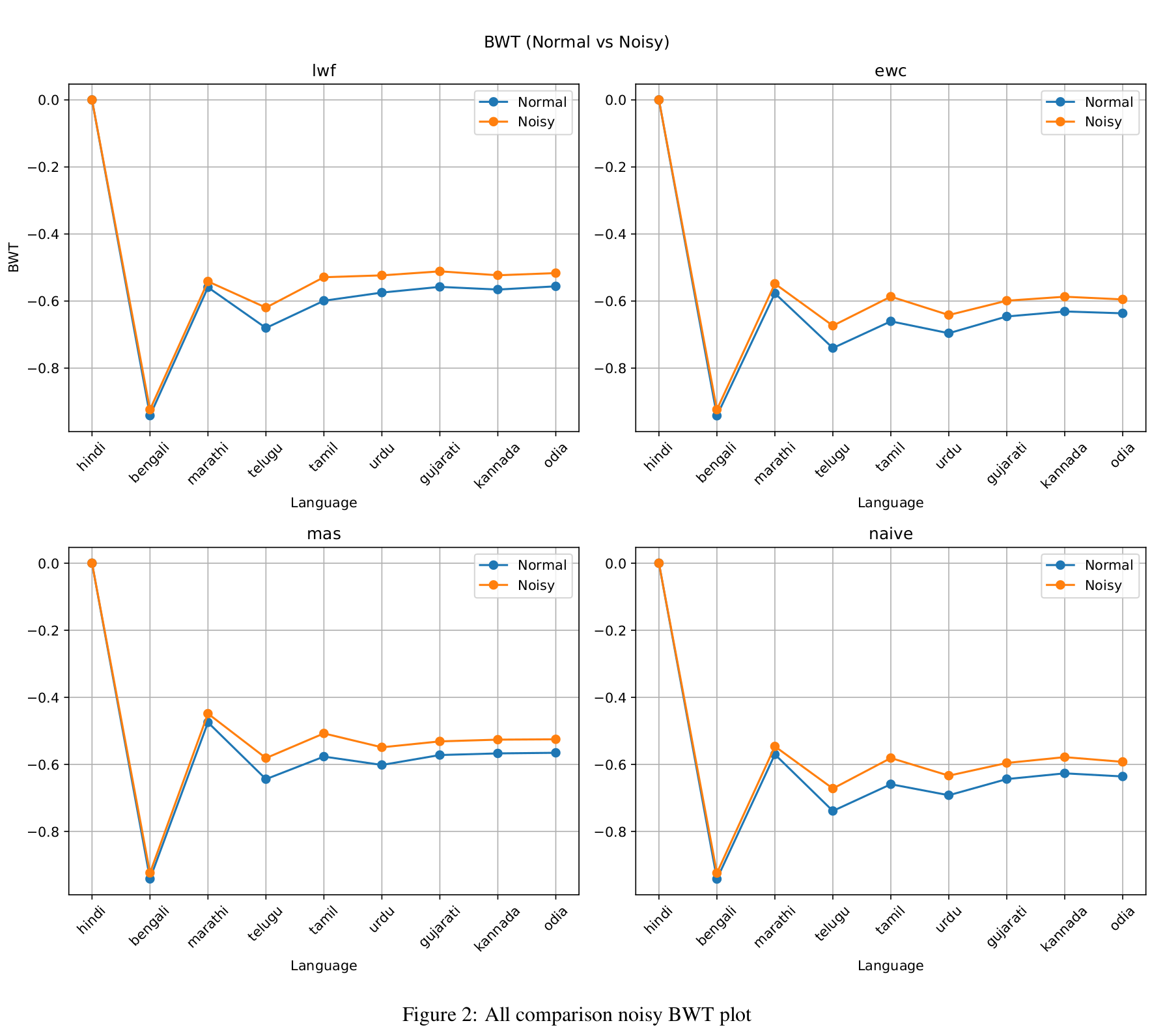
In noisy conditions (Figure 2), both LwF and MAS outperform EWC and the naive baseline in BWT, suggesting better retention of prior knowledge. Interestingly, noise appears to improve backward transfer, likely due to regularization effects. However, this improvement comes with a trade-off: WER increases, and models perform better on clean audio in absolute terms. This contrast indicates that noise can enhance stability, by reducing forgetting, while simultaneously impairing plasticity, by diminishing learning precision, which is reflected in the higher WER.

WER Performance Analysis
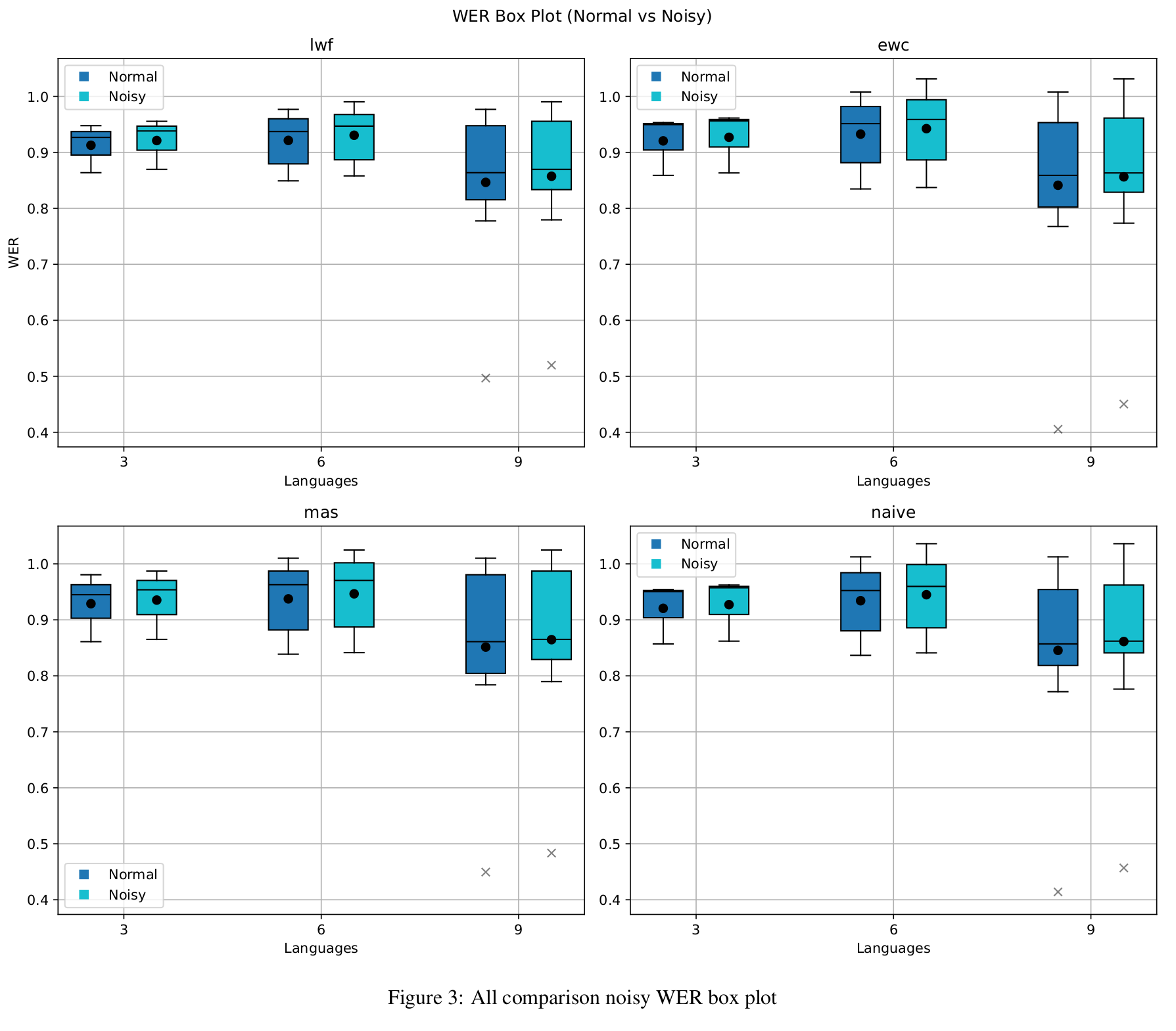
Figures 3 and 4 present WER trends over increasing task lengths. Evaluations are averaged over the last two and current tasks, categorized as short (1–3), medium (1–6), and long (1–9). In general, models perform better with clean data. Among the methods, LwF consistently maintains WER below 1.0, with high stability indicated by narrow shaded variance regions.
Interestingly, the upper bounds of noisy WER for LwF are comparable to the maxima seen under clean conditions. This can be attributed to its distillation-based loss, which prevents overfitting to noisy inputs by anchoring the model to previous predictions. MAS follows a similar pattern, though with slightly lower stability. EWC occasionally achieves better minimum WERs, particularly for short tasks, but continues to show poor BWT. The naive method performs surprisingly well in short sequences but fails to retain knowledge over longer horizons. Overall, LwF demonstrates the effectiveness of knowledge distillation in maintaining a balance between acquiring new knowledge and retaining previous learning. For longer sequences, average WER tends to decline, possibly due to simpler language characteristics in later tasks.
EWC Ablation Studies
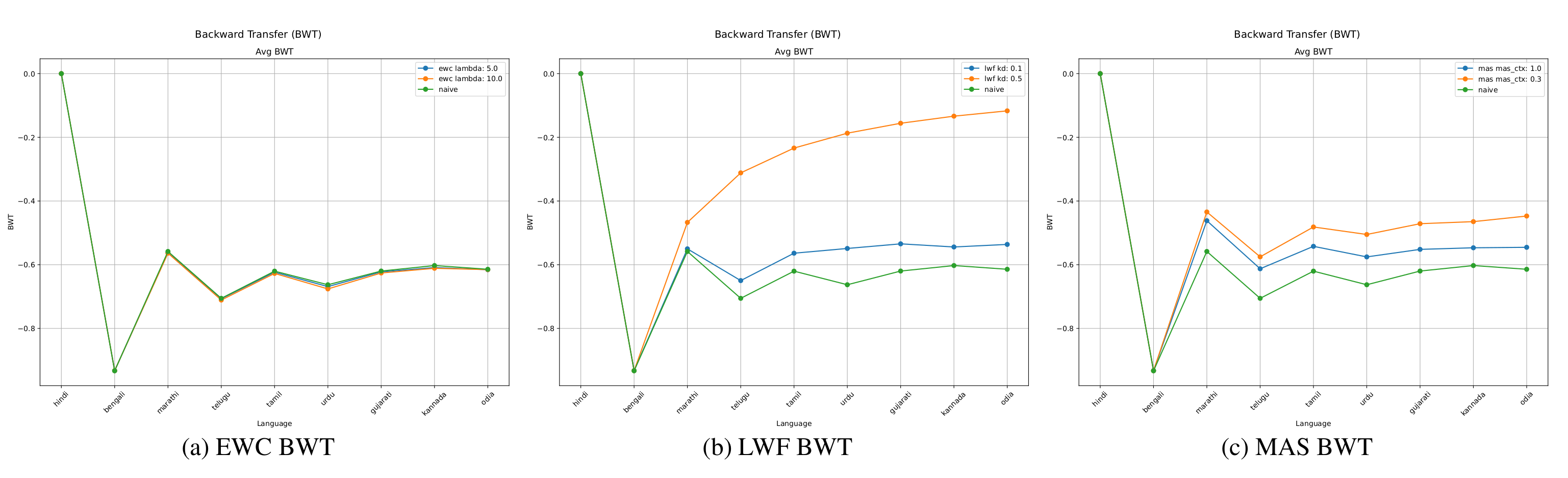
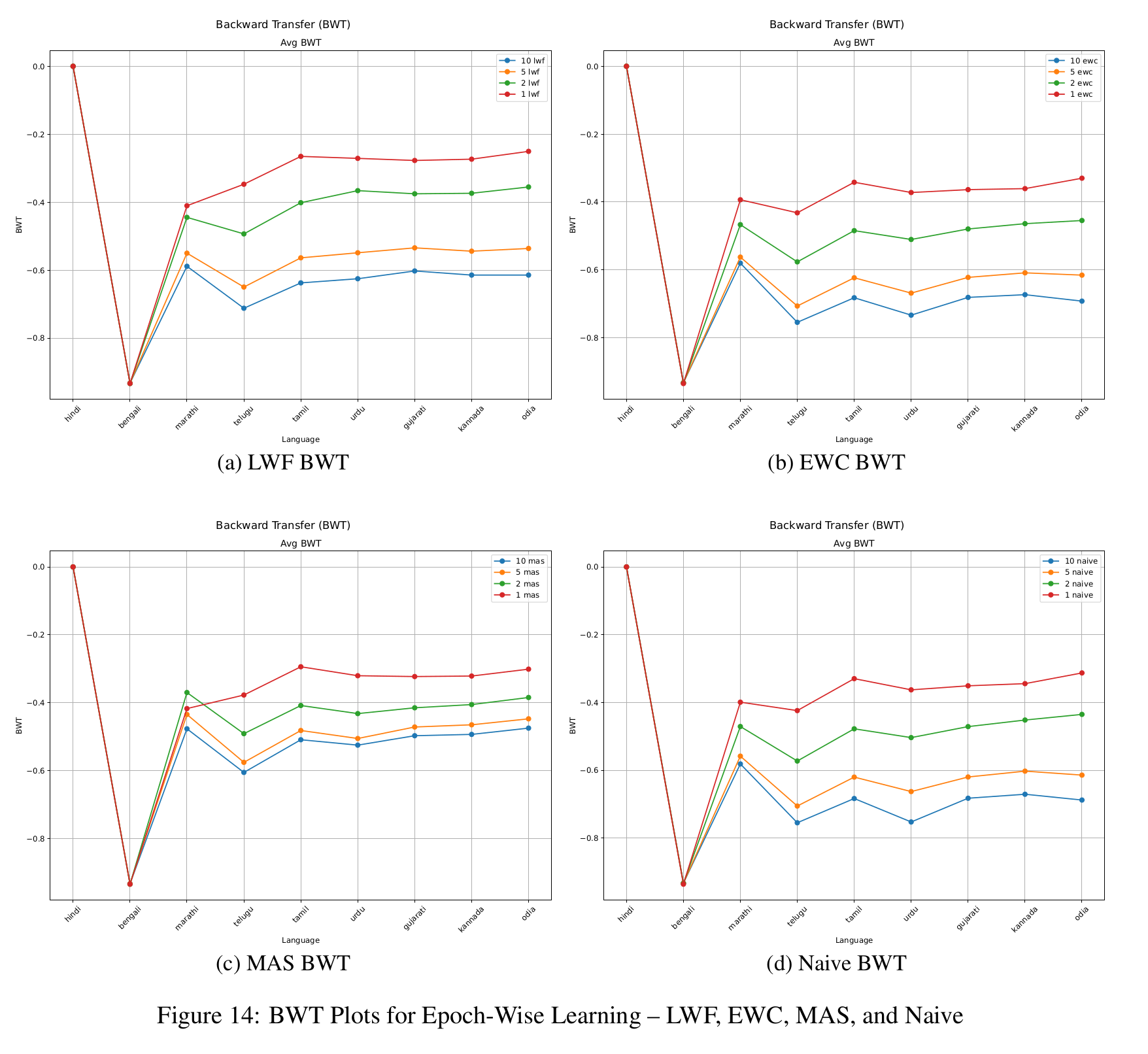
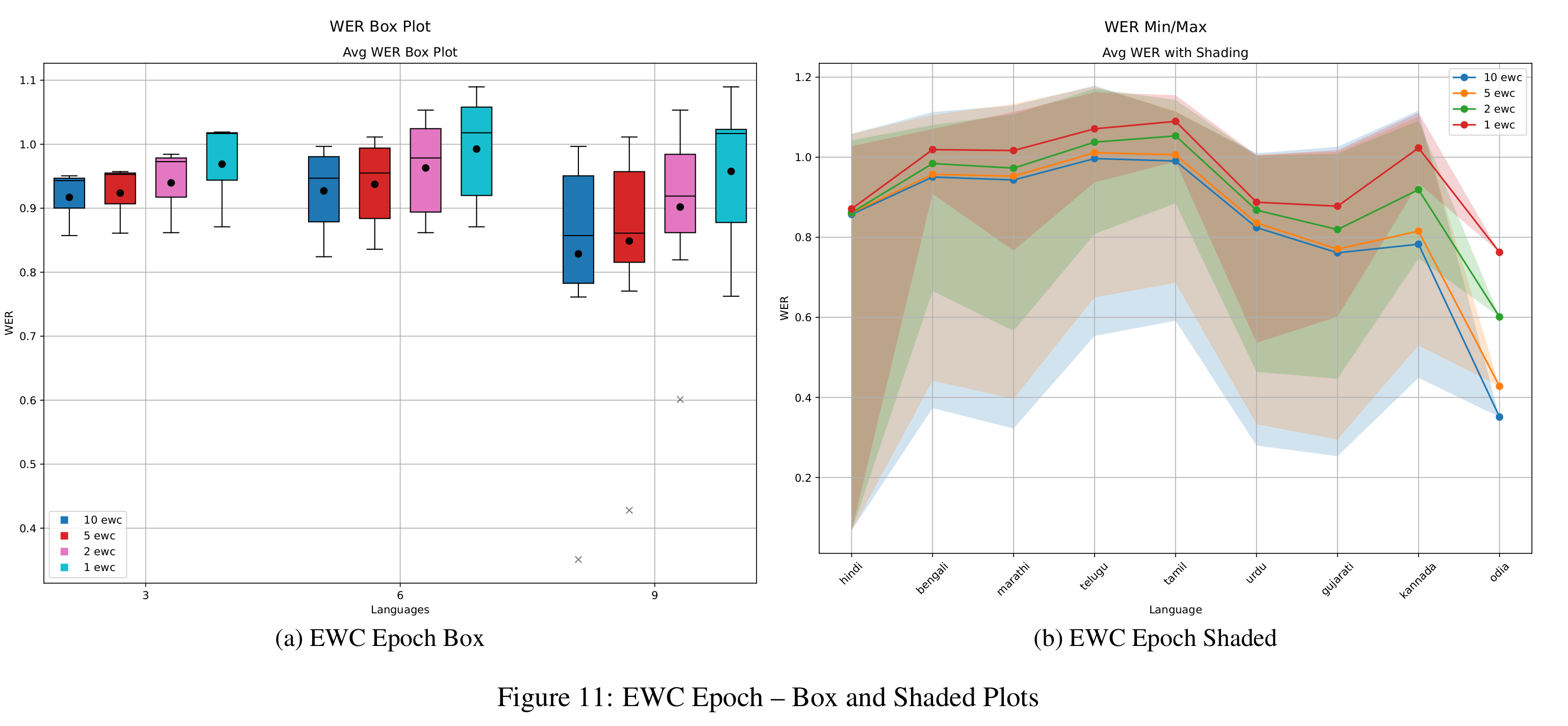
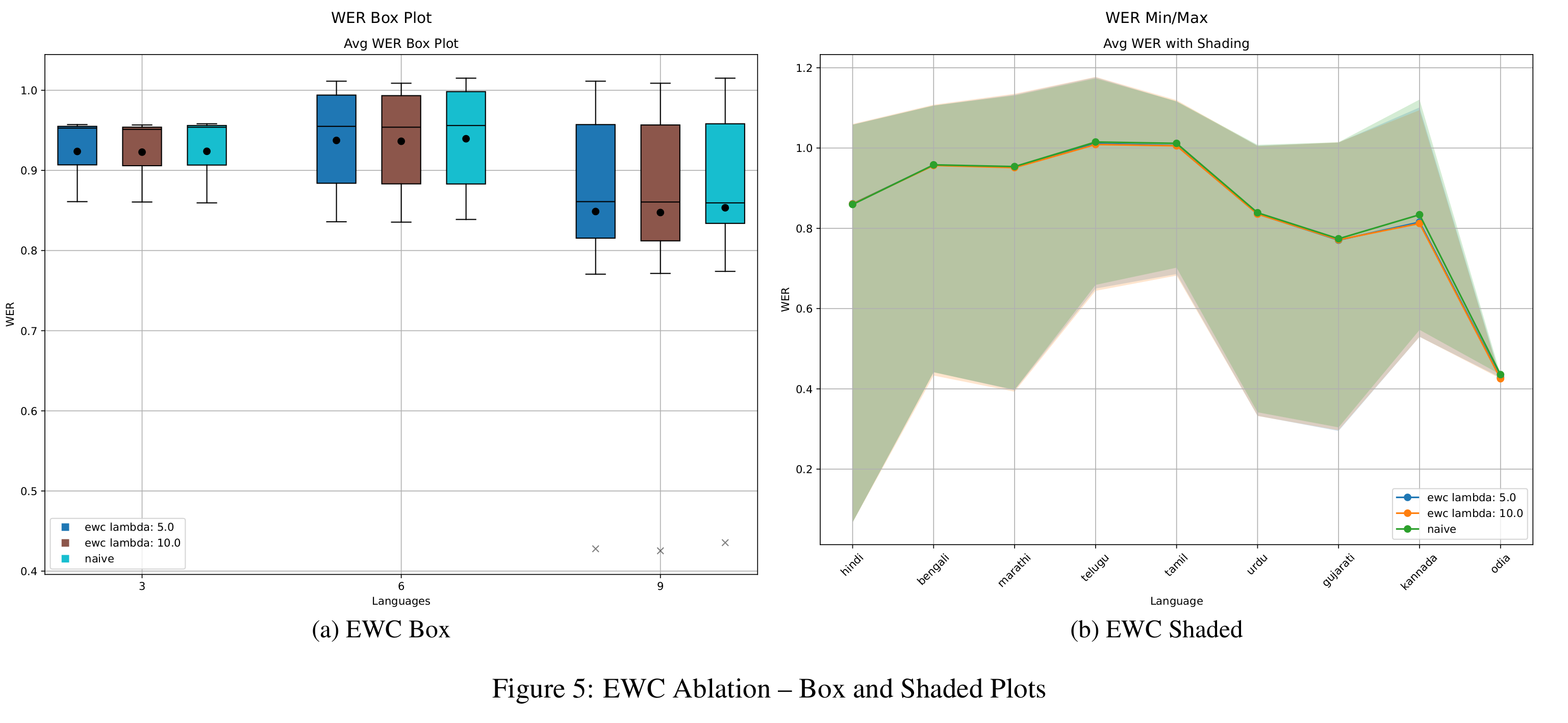
In Figure 5, we examine the impact of different regularization strengths in EWC by testing λEWC ∈ {5, 10}. While both values yield similar outcomes, λEWC = 10 leads to slightly better WER in medium and long tasks, though the benefit is minimal in short tasks. BWT trends (Figure 8) for both values remain close to those of the naive baseline, suggesting limited ability to retain performance on earlier tasks. Additionally, results from epoch-wise ablation (Figure 11) show that increasing training epochs reduces WER, with the best results achieved at epoch 10. However, BWT steadily declines with more epochs (Figure 14), confirming the stability-plasticity trade-off: improved learning on new tasks often leads to increased forgetting of previous ones.
LwF Ablation Studies
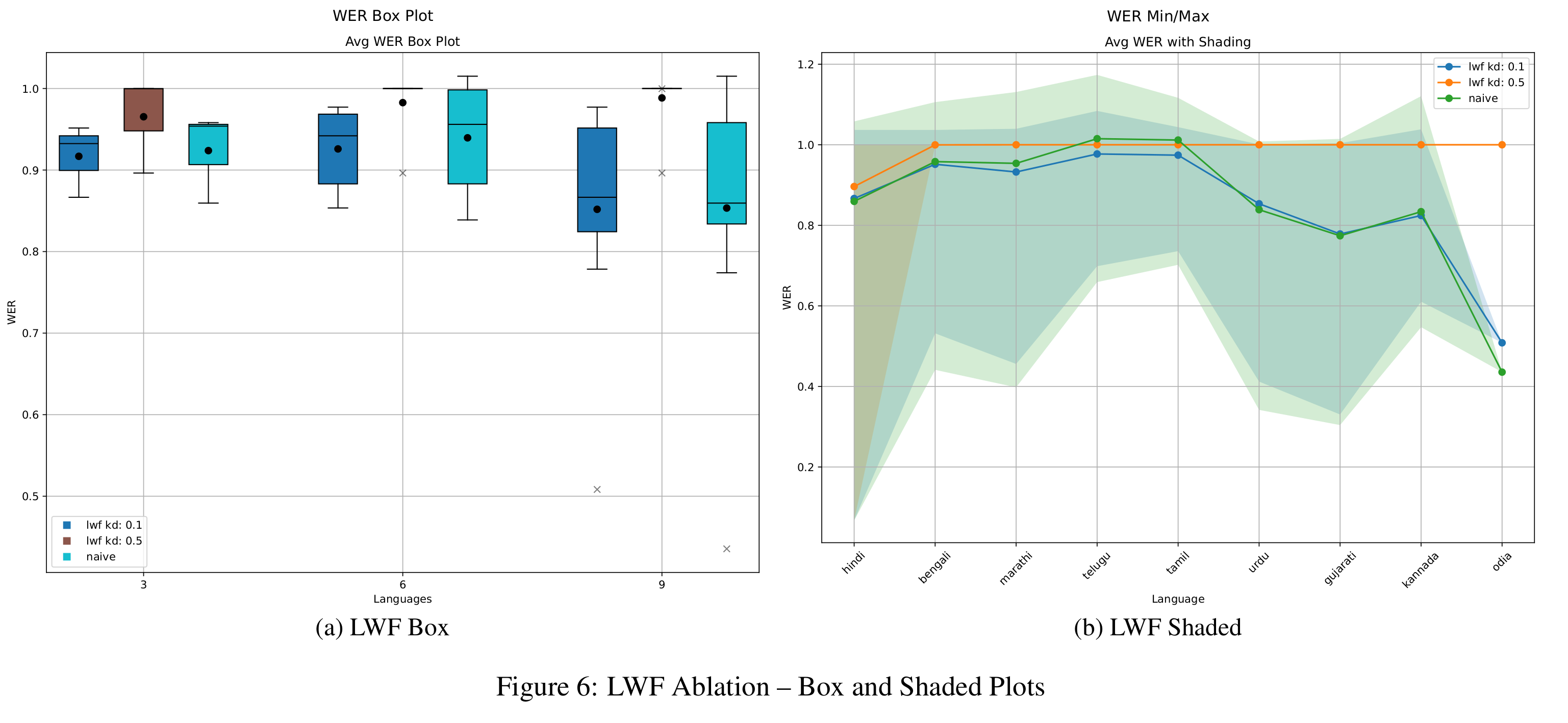
As shown in Figure 6, adjusting the distillation weight αKD significantly impacts LwF’s performance. A higher value of 0.5 severely limits the model’s ability to learn new tasks, resulting in WERs close to 1.0 across all horizons—worse than naive fine-tuning for short sequences. In contrast, αKD = 0.1 strikes a better balance, achieving WER comparable to or better than naive fine-tuning while maintaining much stronger BWT. As shown in Figure 8, the 0.5 configuration yields the highest BWT, primarily because the model barely updates and effectively freezes previous knowledge. The 0.1 setting enables more meaningful learning while controlling forgetting.
Epoch-wise trends (Figures 10 and 14) are consistent with those observed in EWC. Increasing the epochs improves WER but worsens BWT.
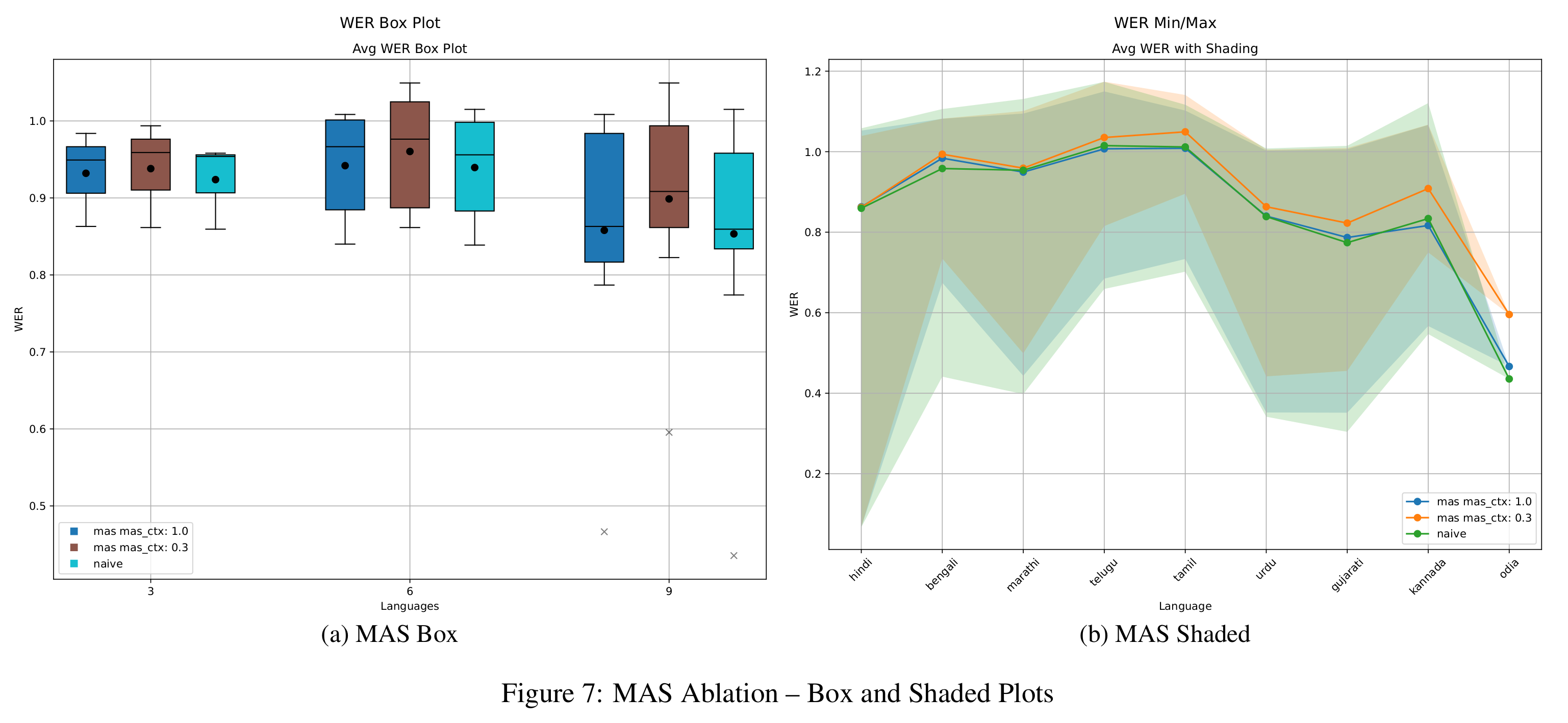
MAS Ablation Studies
In Figure 7, we compare MAS with regularization weights αctx of 0.3 and 1.0. The stronger setting of 1.0 consistently achieves better WER and shows more stable variance across tasks. Its shaded performance region closely overlaps with that of naive fine-tuning, though with lower dispersion. When examining BWT (Figure 8), the 0.3 configuration performs better, matching LwF in retaining knowledge.
As with the other methods, MAS exhibits the stability-plasticity trade-off: increasing epochs (Figure 12) lowers WER but leads to worsening BWT (Figure 14). This consistent trend across methods emphasizes the fundamental challenge in continual learning of effectively balancing the acquisition of new information with the retention of existing knowledge.
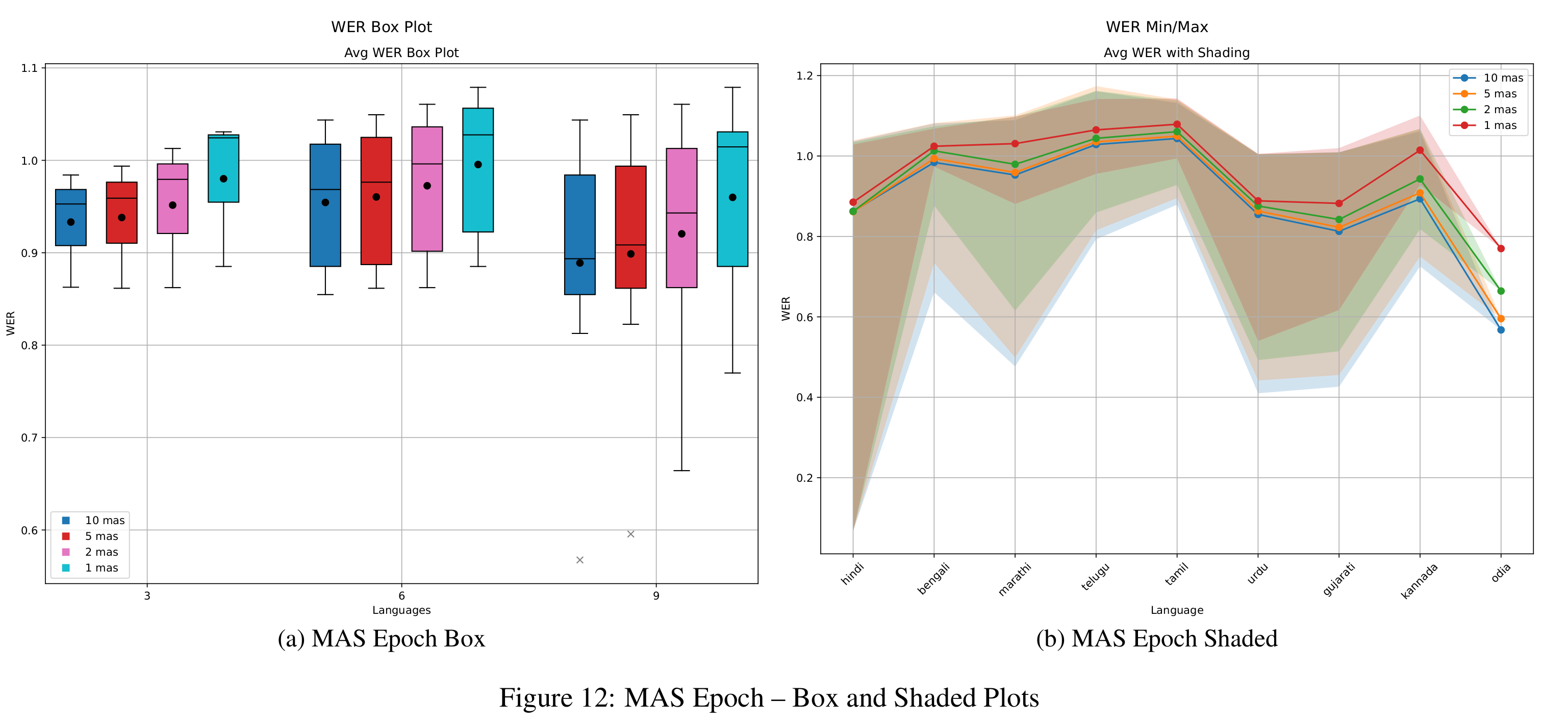

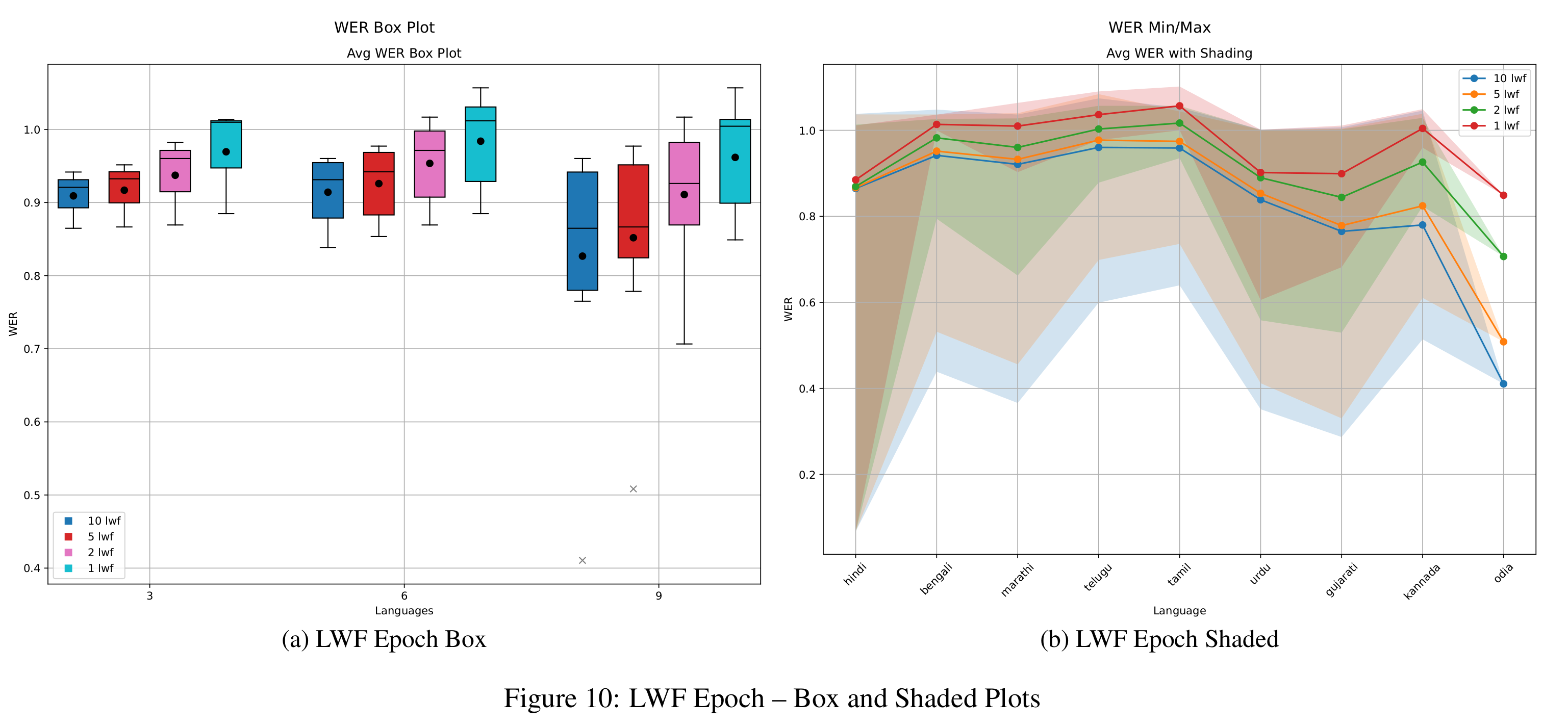





















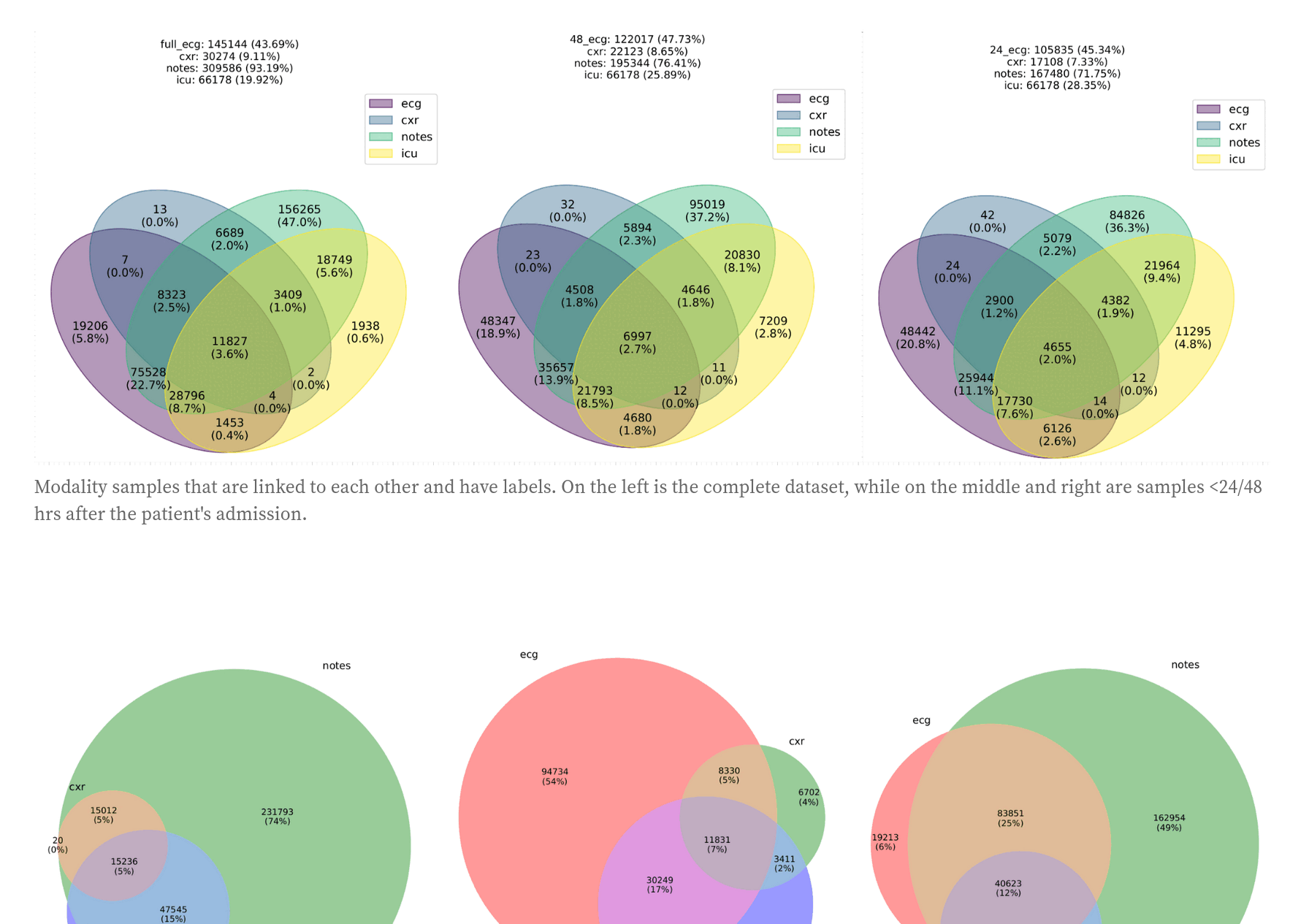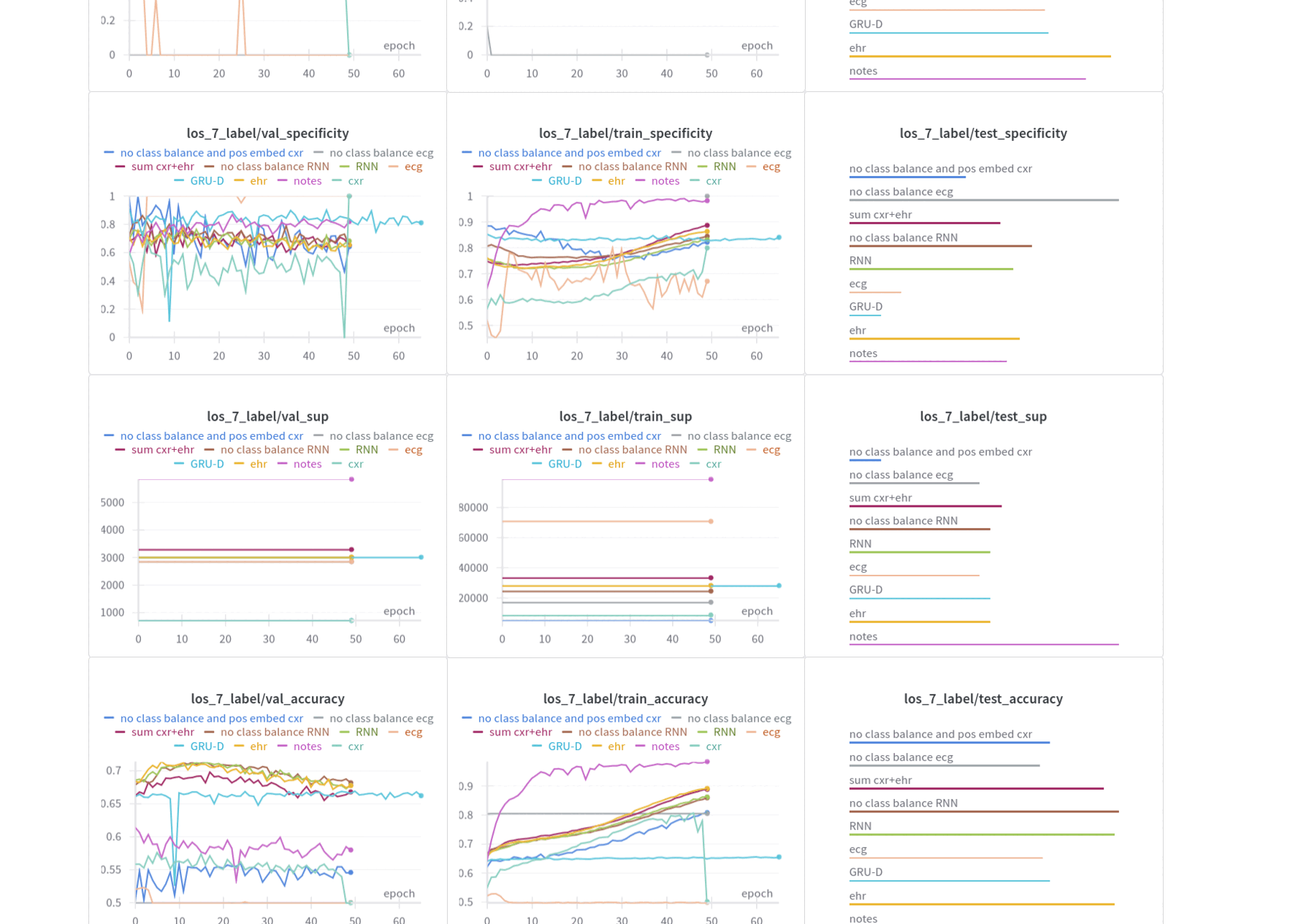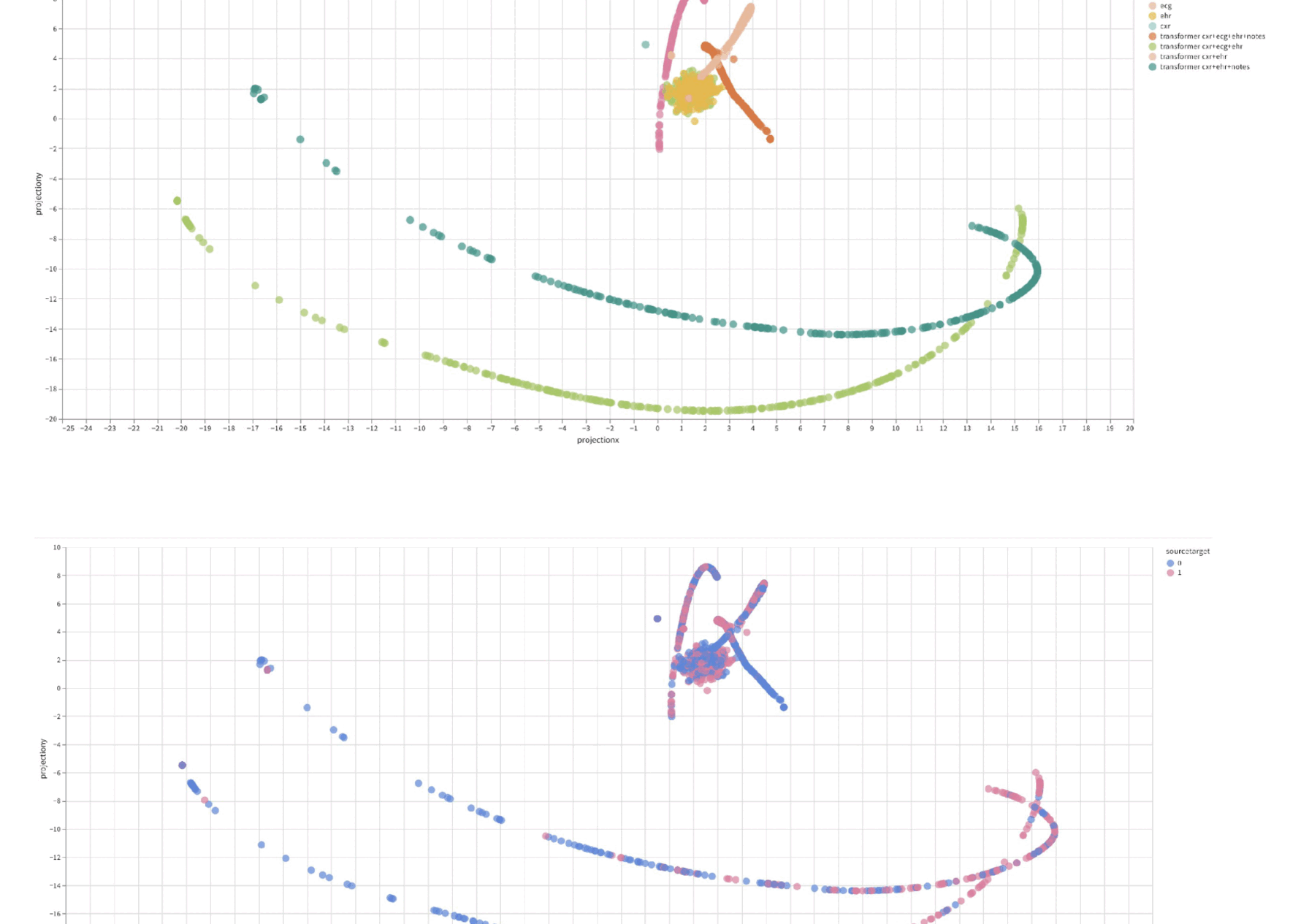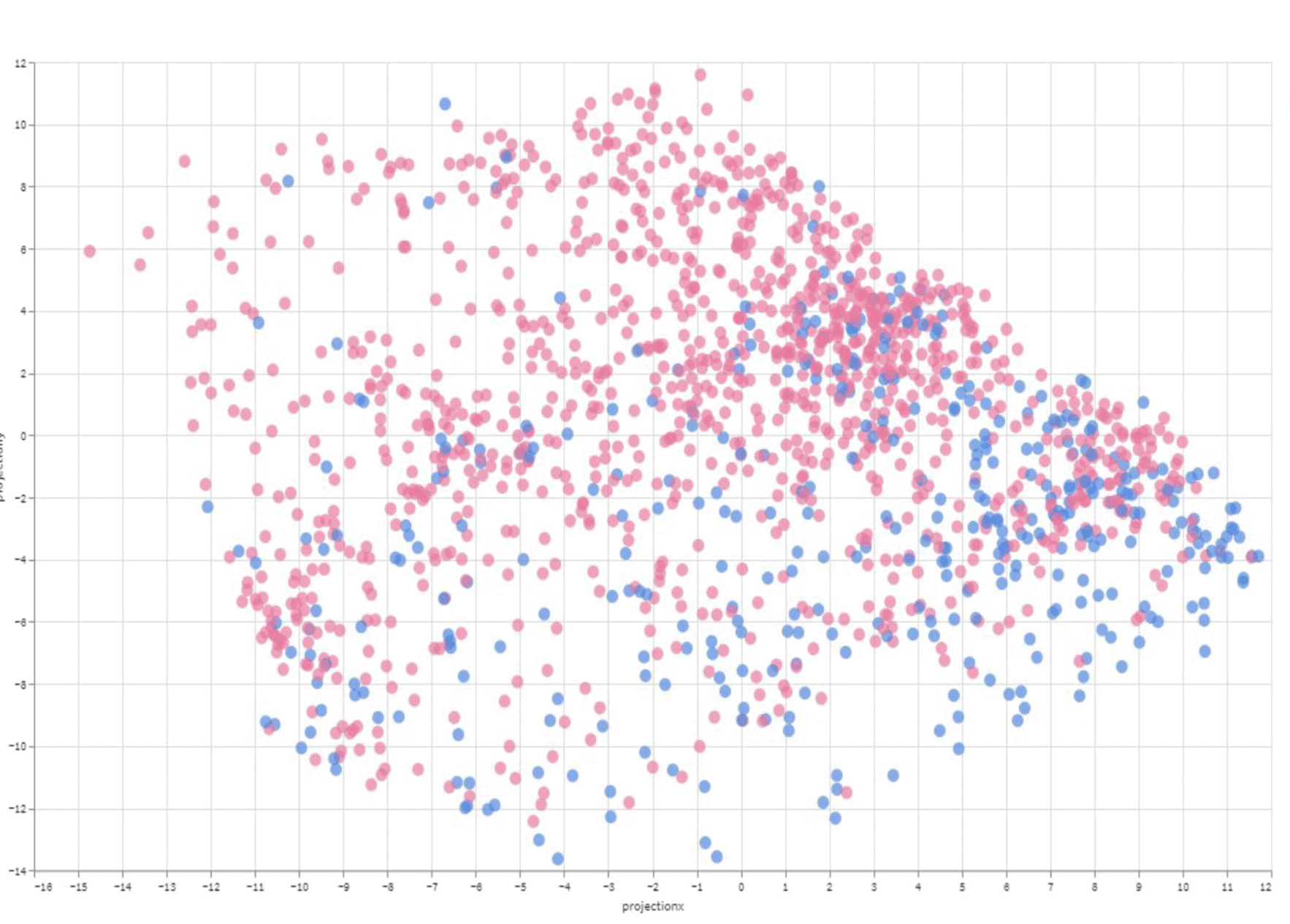


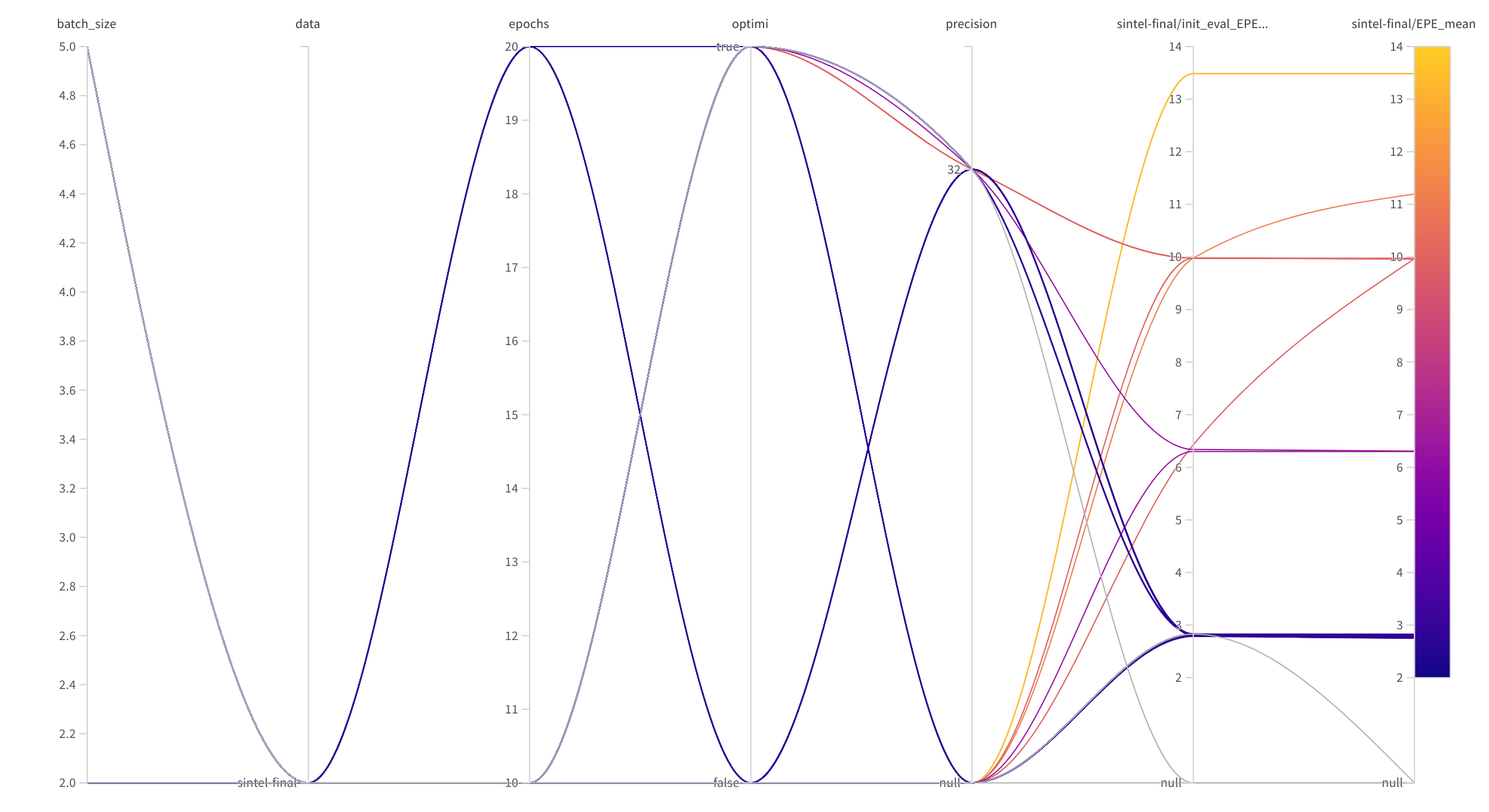

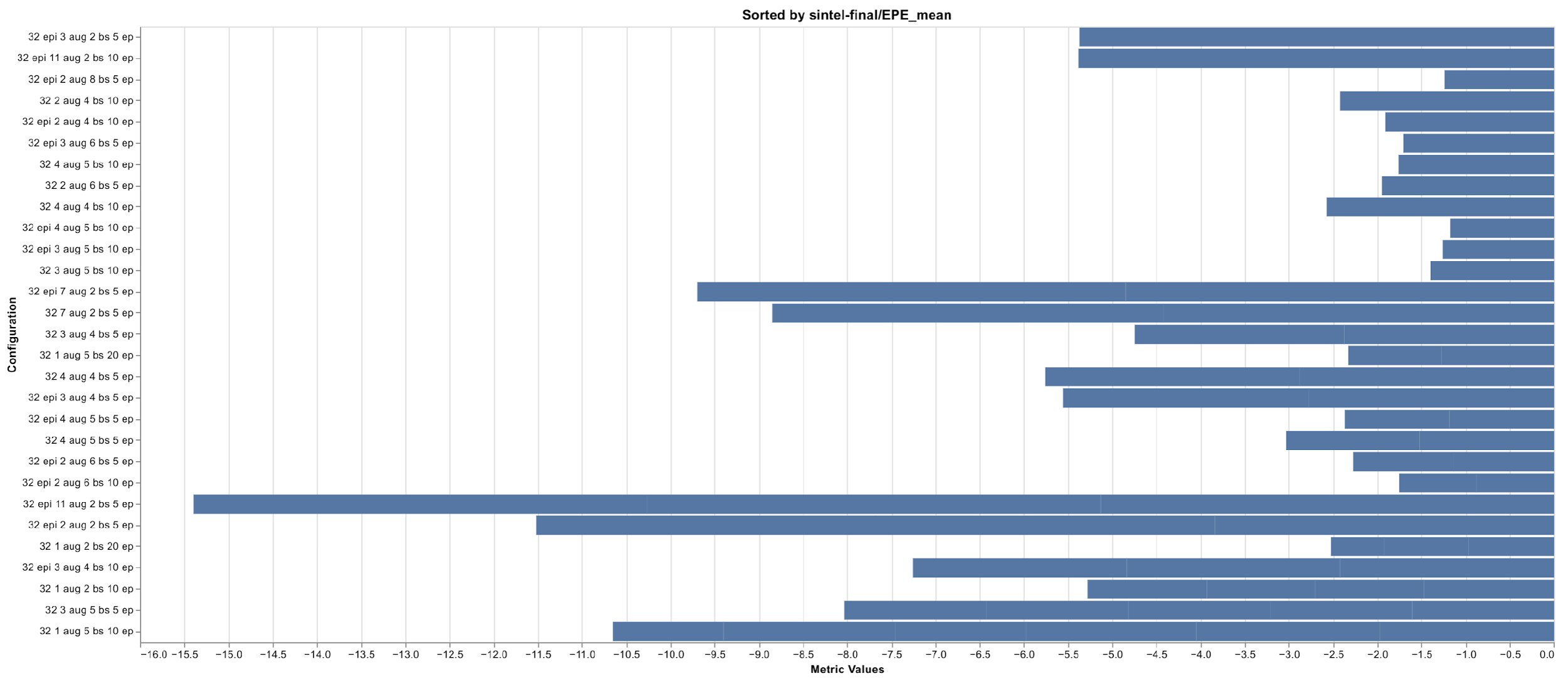 Figure 9: Percentage of absolute EPE score changes
Figure 9: Percentage of absolute EPE score changes 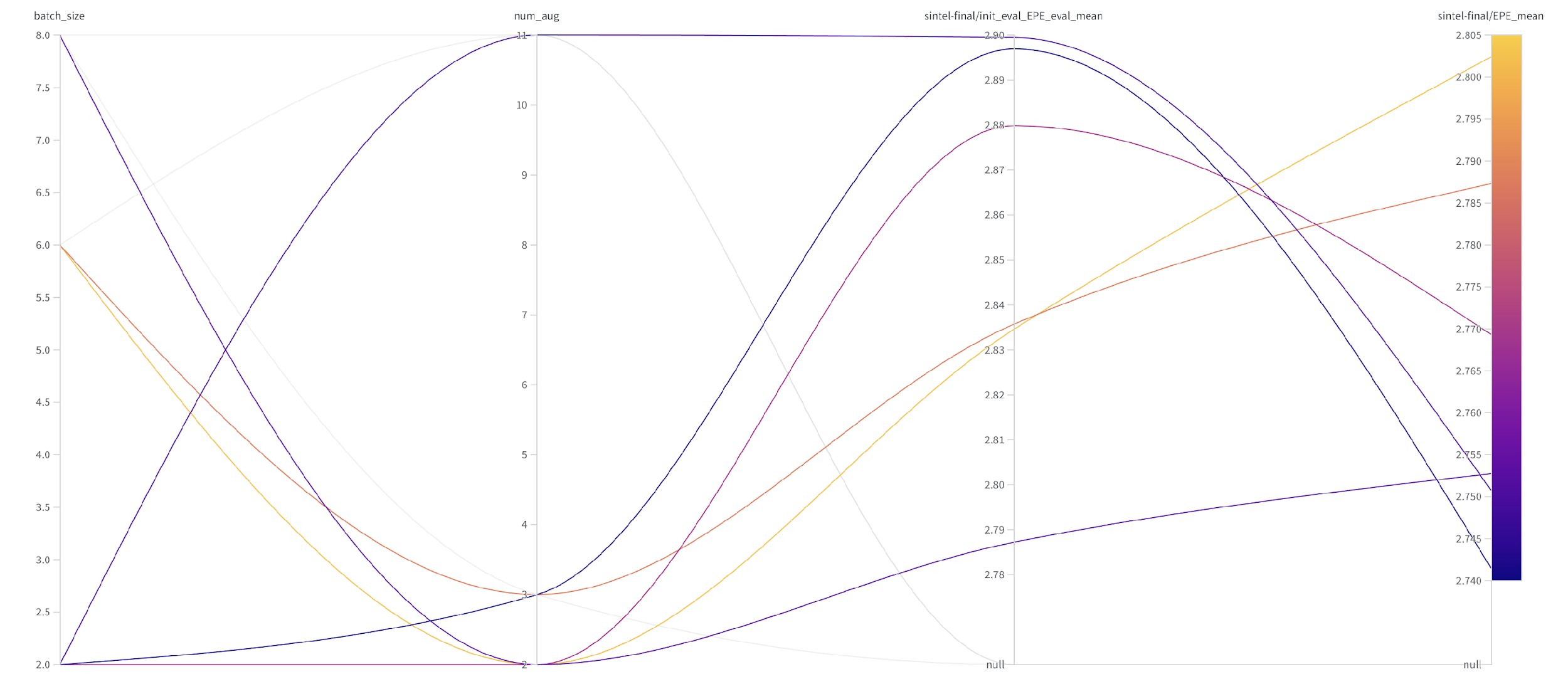 Figure 10: EPE scores for different configurations
Figure 10: EPE scores for different configurations 



 Weights & Biases
Weights & Biases